From Wikipedia, the free encyclopedia
The Monty Hall problem is a probability puzzle based on the American television game show Let’s Make a Deal. The name comes from the show host, Monty Hall. The problem is also called the Monty Hall paradox, as it is a veridical paradox in that the result appears absurd but is demonstrated to be true. [1]
A well-known statement of the problem was published in Parade magazine:
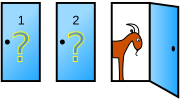
Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice? (Whitaker 1990)
Because there is no way for the player to know which of the two remaining unopened doors is the winning door, most people assume that each of these doors has an equal probability and conclude that switching does not matter. In fact, the player should switch—doing so doubles the probability of winning the car from 1/3 to 2/3.
When the problem and the solution appeared in Parade, approximately 10,000 readers, including nearly 1,000 with Ph.D.s, wrote to the magazine claiming the published solution was wrong. Some of the controversy was because the Parade version of the problem is technically ambiguous since it leaves certain aspects of the host’s behavior unstated, for example, whether the host must open a door and must make the offer to switch. Variants of the problem involving these and other assumptions have been published in mathematical literature.
The standard Monty Hall problem is mathematically equivalent to the earlier Three Prisoners problem and both are related to the much older Bertrand’s box paradox. These and other problems involving unequal distributions of probability are notoriously difficult for people to solve correctly, and have led to numerous psychological studies. Even when given a completely unambiguous statement of the Monty Hall problem, explanations, simulations, and formal mathematical proofs, many people still meet the correct answer with disbelief.